桶排序、计数排序、基数排序-PySuper

非基于比较的排序，与被排序的样本的实际数据状况很有关系，所以实际中并不经常使用

时间复杂度O(N)，额外空间复杂度O(N)

稳定的排序

桶排序

给定一个数组，求如果排序之后，相邻两数的最大差值

要求时间复杂度O(N)，且要求不能用非基于比较的排序。

N个数，准备N + 1个桶
找到数组中的最小值，和最大值（如果相等，则差值为0）
把min放在第一个桶，max放在最后一个桶，将数组等分成N+1个数组
数在哪个范围，就放在哪个桶
- 第一个桶和最后一个桶都非空，那在这之间一定存在一个非空桶
- 相邻两数可能来自同一个桶，也可能来自相邻两桶
- 空桶左侧桶的最大值，空桶右侧桶的最小值==> 两者差值一定大于桶所表示的范围
- 所以，最大差值一定是空桶左侧桶的最大值，空桶右侧桶的最小值，二者差值
记录每个桶的三个值：最小值、最大值、是否有值
每一个非空桶，都找它左边的最近的非空桶，差值：min右-max左

class MaxGap:
    def get_max(self, arr: list):
        """启动桶排序"""
        if arr is None or len(arr) < 2:
            return 0

        # 拿到数组中的最大值最小值
        min_, max_, len_ = min(arr), max(arr), len(arr)
        for num in arr:
            min_, max_ = min(min_, num), max(max_, num)
        if min_ == max_:  # 说明只有一个相同的数
            return 0

        min_s = [0] * (len(arr) + 1)  # 每个桶的最小值
        max_s = [0] * (len(arr) + 1)  # 每个桶的最大值
        has_num = [0] * (len(arr) + 1)  # 当前桶中是否有数值

        # 当前数去第几号桶，修改这个桶的最小值，最大值，是否有值
        for i in range(len(arr)):
            bid = self.bucket(arr[i], len_, min_, max_)  # TODO: 几号桶
            min_s[bid] = min(min_s[bid], arr[i]) if has_num[bid] else arr[i]
            max_s[bid] = max(max_s[bid], arr[i]) if has_num[bid] else arr[i]
            has_num[bid] = True

        result = 0
        lastMax = max_s[0]

        # 找到每一个非空桶，以及当前非空桶左侧最近的非空桶，用当前痛的最小 - 上一个桶的最大
        for i in range(1, len_):
            if has_num[i]:
                result = max(result, min_s[i] - lastMax)
                lastMax = max_s[i]
        return result

    def bucket(self, num: int, len_: int, min_: int, max_: int):
        """
        怎么确定一个数来自于哪个桶:
            # 最后的的答案一定大于等于 bucket_size
            # 因为只有这n个数均匀排列才等于bucket_size
            # 否则一定大于bucket_size
        """
        return int((num - min_) * (len_ - 1) / (max_ - min_))


list_ = [2, 10, 9, 30]
number = MaxGap().get_max(list_)
print(number)

计数排序

计数排序的核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。

作为一种线性时间复杂度的排序，计数排序要求输入的数据必须是有确定范围的整数。

$注册$

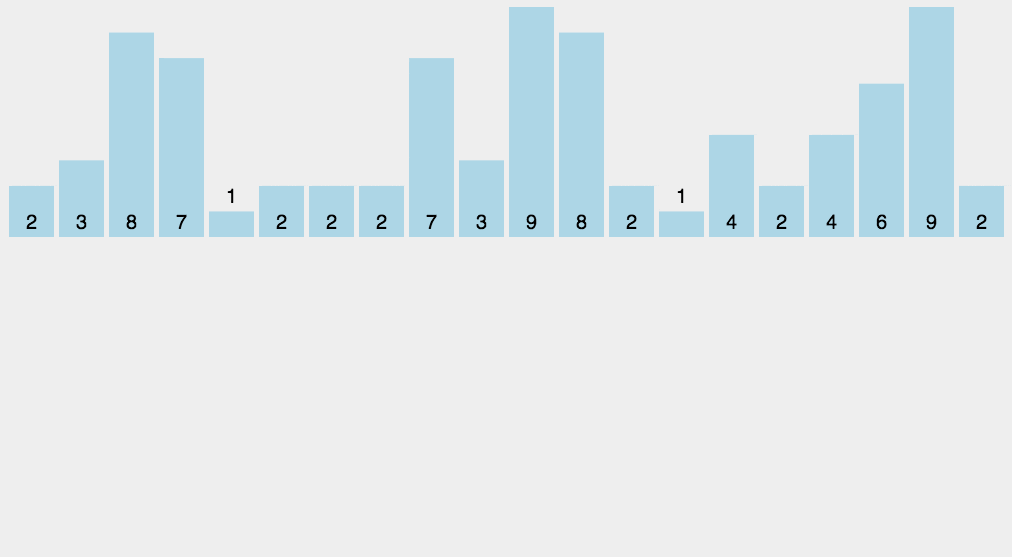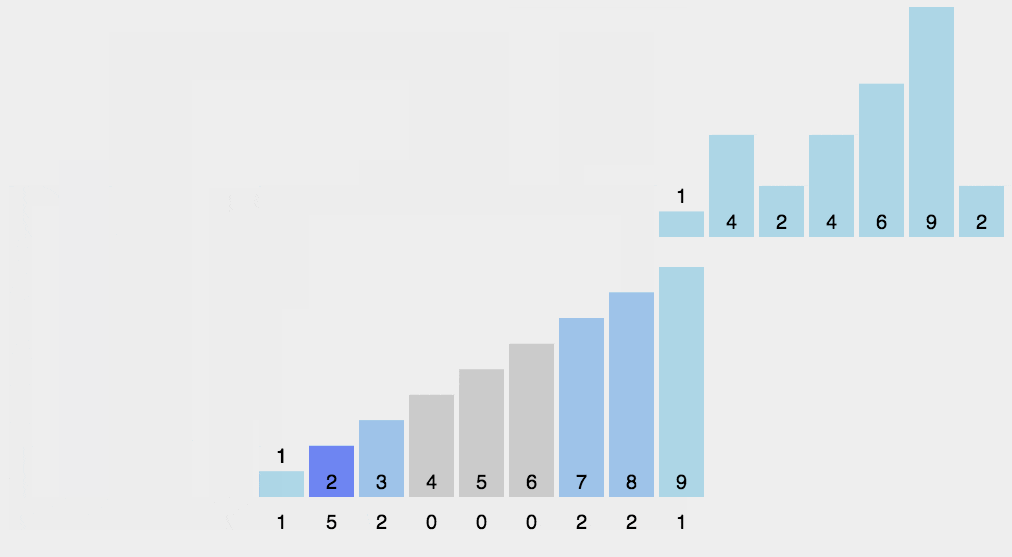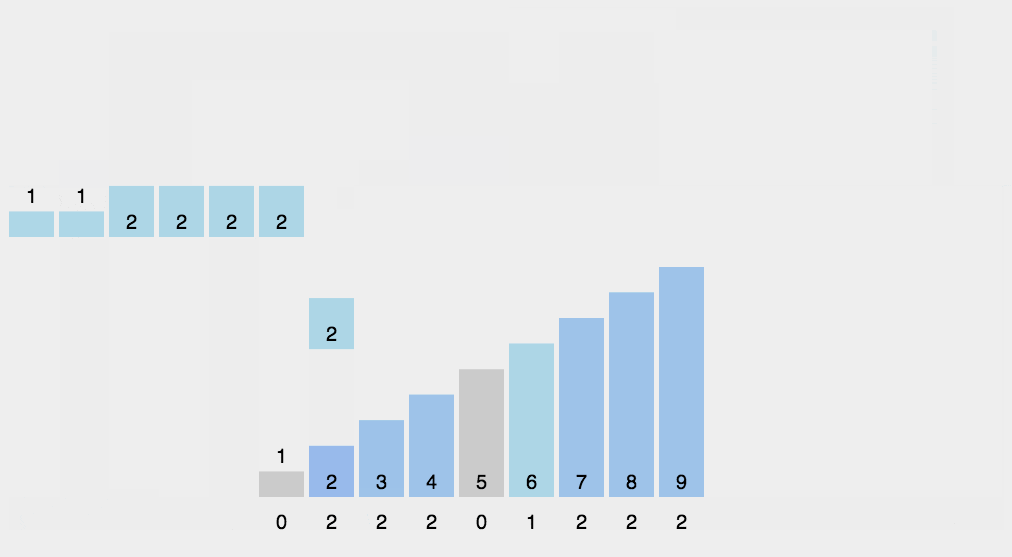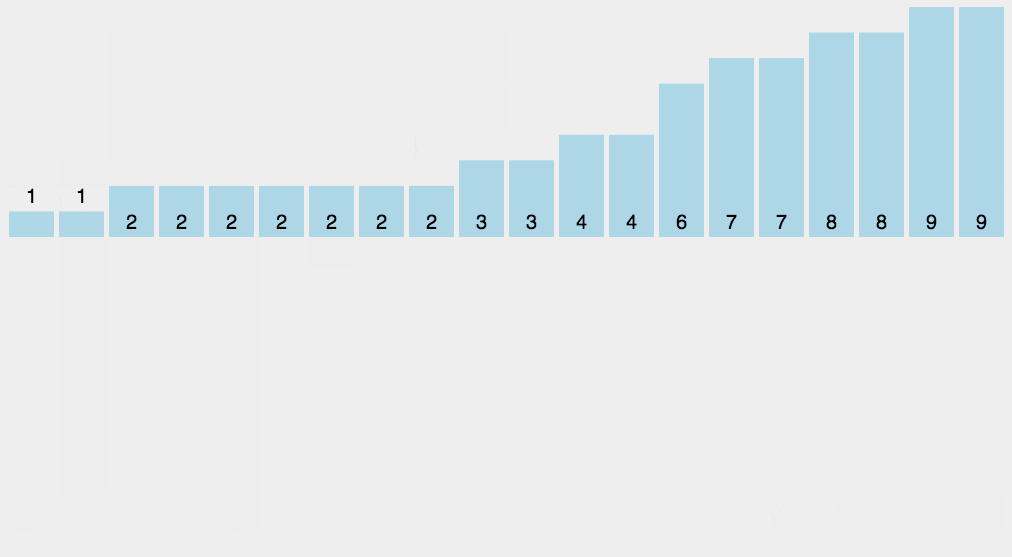
def count_sort(arr):
    output = [0 for i in range(256)]
    count = [0 for i in range(256)]
    ans = ["0" for _ in arr]

    for i in arr:
        count[ord(i)] += 1

    for i in range(256):
        count[i] += count[i - 1]

    for i in range(len(arr)):
        output[count[ord(arr[i])] - 1] = arr[i]
        count[ord(arr[i])] -= 1

    for i in range(len(arr)):
        ans[i] = output[i]
    return ans

arr = "wwwrunoobcom"
ans = count_sort(arr)
print ( "字符数组排序 %s"  %("".join(ans)) )

目录CONTENT

桶排序、计数排序、基数排序

桶排序

计数排序

基数排序

评论区