二叉树
树
树是一种数据结构,它是由n(n>=1)个有限节点组成一个具有层次关系的集合。
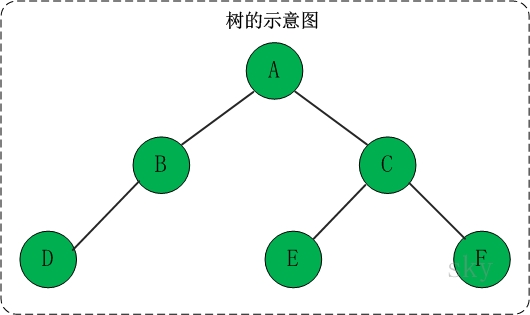
- 树的特点:
- 每个节点有零个或多个子节点
- 没有父节点的节点称为根节点
- 每一个非根节点有且只有一个父节点
- 除了根节点外,每个子节点可以分为多个不相交的子树
- 树的术语:
结点的度:结点拥有的子树的数目。叶子:度为零的结点。分支结点:度不为零的结点。树的度:树中结点的最大的度。层次:根结点的层次为1,其余结点的层次等于该结点的双亲结点的层次加1。树的高度:树中结点的最大层次。无序树:如果树中结点的各子树之间的次序是不重要的,可以交换位置。有序树:如果树中结点的各子树之间的次序是重要的, 不可以交换位置。森林:0个或多个不相交的树组成。对森林加上一个根,森林即成为树;删去根,树即成为森林。
二叉树
每个节点最多有两个子树的树结构
- 五种基本形态:
- 跟和左右子树
- 二叉树可以是空集
- 根可以有空的左子树
- 根可以有空的右子树
- 左、右子树皆为空
<img src=“http://qny.zhengxingtao.com/media/images/BST_2.jpg”/ style=“max-width: 93%;”>
- 二叉树有以下几个性质:
- 二叉树第i层上的结点数目最多为 2{i-1} (i≥1)。
- 深度为k的二叉树至多有2{k}-1个结点(k≥1)。
- 包含n个结点的二叉树的高度至少为log2 (n+1)。
- 在任意一棵二叉树中,若终端结点的个数为n0,度为2的结点数为n2,则n0=n2+1
案例
给定一个二叉树,判断其是否是一个有效的二叉搜索树
- 一个二叉搜索树具有如下特征:
- 节点的左子树只包含小于当前节点的数
- 节点的右子树只包含大于当前节点的数
- 所有左子树和右子树自身必须也是二叉搜索树
class Solution(object):
"""
从上往下比较的,将每个节点往左就是最大,往右就是最小值
在传输过程中原函数不能够传递最大最小值,又重新定义了一个函数调用
"""
def validBST(self, root, min, max):
if root == None:
return True
if root.val <= min or root.val >= max:
return False
return self.validBST(root.left, min, root.val) and self.validBST(root.right, root.val, max)
def isValidBST(self, root):
"""
:type root: TreeNode
:rtype: bool
"""
return self.validBST(root, -21474836480, 21474836470)
递归
之前我对于需要重复使用的一个方法,总是使用回调的方式处理,而算法有种类似的处理方式–递归
递归就是在函数内部调用自己的函数被称之为递归
个人感觉
递归就像是套娃
- 递归的特点:
- 必须有一个明确的结束条件
- 每次进入更深一层递归时,问题规模(计算量)相比上次递归都应有所减少
- 递归效率不高,递归层次过多会导致栈溢出
在计算机中,函数调用是通过栈(stack)这种数据结构实现的,每当进入一个函数调用,栈就会加一层栈帧,每当函数返回,栈就会减一层栈帧。由于栈的大小不是无限的,所以,递归调用的次数过多,会导致栈溢出
def recursion(n):
"""将 10不断除以2,直至商为0,输出这个过程中每次得到的商的值"""
# 每次求商,输出商的值
v = n//2
print(v)
if v==0:
return 'Done' # 当商为0时,停止,返回Done
# 递归调用,函数内自己调用自己
v = recursion(v)
recursion(10) # 函数调用
递归与非递归的对比
# 非递归实现阶乘
def factorial(n):
res = 1
for i in range(2, n+1):
res *= i
return res
print(factorial(4))
# 递归实现阶乘
def factorial(n):
if n == 0 or n == 1:
return 1
else:
return (n * factorial(n - 1))
print(factorial(5))
二分法
给定一个有序列表,获取其索引
index()
直接使用index获取,如果
i比较靠前,那么遍历列表的次数还可以接受
但是如果列表很长,同时 i 也在最后,这时的遍历就很费事了(
时间复杂度)
def index_search(items, i):
"""使用内置方法,获取索引"""
for num in items:
if num == i:
return items.index(num)
可变类型
列表是可变类型
我们遍历列表的同时队列表进行操作,第二次遍历的时候,列表会变成我们操作后的列表
def change_search(items, i):
"""未做是否在列表中的判断"""
# 队列表删除后,列表中少一个值,通过计数获取在原列表中的index
x = 0
for num in items:
if i > num:
items.remove(num)
elif i < num:
# 每次删除一个,间隔一个,所以出现比 i 小的,那么 i 就一定在前一个
return items.index(num) - 1 + x
else: # i = num
return items.index(num) + x
x += 1
二分法
二分法可以减少很多的比较次数
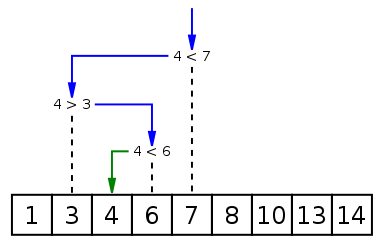
def binary_search(items, left, right, i):
"""二分查找: 对列表进行切片,每次比较确定 i 在左边还是右边"""
# 判断是否在列表中
if right >= left:
mid = int(left + (right - left) / 2)
# 刚好取到 i
if items[mid] == i:
return mid
# i 小于中间位置的元素,只需要再比较左边的元素
elif items[mid] > i:
return binary_search(items, left, mid - 1, i)
# i 大于中间位置的元素,只需要再比较右边的元素
else:
return binary_search(items, mid + 1, right, i)
else:
# 不存在
return " {} 不在列表中!".format(i)
i = 7
items = [1, 2, 3, 4, 5, 6, 7, 8, 9]
result = binary_search(items, 0, len(items) - 1, i)
print(result)





评论区